Tan 2x ≠ 2 tan x by Shavana GonzalezIdentity\\cos(2x) identity\\tan(2x) multipleangleidentitiescalculator identity \tan(2x) en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identityLegend x and y are independent variables, ;

What Is The Integration Of Tan 2x Solution Quora
Tan 2x identity
Tan 2x identity- To evaluate this integral, let's use the trigonometric identity sin2x = 1 2 − 1 2cos(2x) Thus, ∫sin2xdx = ∫ (1 2 − 1 2cos(2x))dx = 1 2x − 1 4sin(2x) C Exercise 723 Evaluate ∫cos2xdx Hint cos 2 x = 1 2 1 2 cos ( 2 x) Answer ∫ cos 2 x d x = 1 2 x 1 4 sin ( 2 x) CCos 2x ≠ 2 cos x;




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
Get an answer for 'Prove tan^2x sin^2x = tan^2x sin^2x' and find homework help for other Math questions at eNotes How to prove the identity `sin^2x cos^2x = 1` ?Proving Trigonometric Identities Calculator Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!Formulas and Identities Tangent and Cotangent Identities sincos tancot cossin qq qq qq == Reciprocal Identities 11 cscsin sincsc 11 seccos cossec 11 cottan tancot qq qq qq qq qq qq == == == Pythagorean Identities 22 22 22 sincos1 tan1sec 1cotcsc qq qq qq = = = Even/Odd Formulas ( ) ( ) ( ) ( ) ( ) ( ) sinsincsccsc coscossecsec tantancotcot qqqq
Trigonometric Identities Solver \square!The half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify the identity tan (α/2) = (1 − cos α)/sin α Example 7 Verify the identity tan (α − 2) = sin π/(1 cos α)Trigonometric identities Intro to Pythagorean trigonometric identities Converting between trigonometric ratios example write all ratios in terms of sine Practice Evaluating expressions using basic trigonometric identities Trigonometric identity example proof involving sec, sin, and cos
Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x Sin 2x = Sin 2x = sin(2x)=2sin(x) cos(x) Sin(2x) = 2 * sin(x)cos(x) Proof To express Sine, the formula of "Angle Addition" can be usedD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube



What Is The Formula Of Tan2x Quora
1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!Tan2x Formula Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = 2 tan x 1 − t a n 2 xFree math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantly



7 Proving Ids Trig Functions Identities




Tan 2x Formula What Is Tan 2x Formula Examples
Identidade\\tan(2x) doubleangleidentitiescalculator identity \tan(2x) pt Related Symbolab blog posts Spinning The Unit Circle (Evaluating Trig Functions )Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx mathematics evaluate each of the followingsin 130tan 60/cos 540tan 230sin 400 Precalculus help I have two problems I am stuck on, if you could show me how to solve the problems it would be I'm currently stumped on proving the trig identity below $\tan(2x)\tan (x)=\frac{\tan (x)}{\cos(2x)}$ Or, alternatively written as $\tan(2x)\tan (x)=\tan (x)\sec



Trigonometric Functions Expressed By The Tangent Of The Half Angle Trigonometric Identities



Prove Sin2x 2tanx 1 Tan 2x Socratic
Question Verify The Identity Sec?xtan 2x = Sec X Tan X Secx Tan X Which Sequence Of Steps Verifies The Identity?Verify the Identity tan(2x)^2sin(2x)^2cos(2x)^2=sec(2x)^2 Start on the left side Apply Pythagorean identity Tap for more steps Apply pythagorean identity Apply pythagorean identity Because the two sides have been shown to be equivalent, the equation is an identity is an identityYou have seen quite a few trigonometric identities in the past few pages It is convenient to have a summary of them for reference These identities mostly refer to one angle denoted θ, but there are some that involve two angles, and for those, the two angles are denoted α and β The more important identities



Trig Identities Hsn Forum




Topic Lesson Trigonometric Functions
Work on the right hand side to make it the same as the left hand side = change to sinx and cosx = common denominator = common factor = basic trig identity For questions 1 – 5, decide whether the equation is a trigonometric identity Explain your reasoning cos2 x(1 tan2 x) = 1 sec x tan x(1 – sin2 x) = sin x csc x(2sin x √2) = 0 cos2(2x) – sin2(2x) = 0 sin2 θ csc2 θ = sin2 θ cos2 θTherefore in mathematics as well as in physics, such formulae are useful for deriving many important identities The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is




What Is The Integration Of Tan 2x Solution Quora




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube
108 Educator answers Math Now we can just plug f(x) and g(x) into the chain rule But before we do that, just a quick recap on the derivative of the tan function The derivative of tan(x) with respect to x is sec 2 (x) The derivative of tan(z) with respect to z is sec 2 (z) In a similar way, the derivative of tan(2x) with respect to 2x is sec 2 (2x) We will use this fact as part of the chain rule to find theIs Tan 2 X Sec 2 X 1 An Identity Is tan 2 x ?




What Is Integral Of Sin2x Tan2x Quora




Weierstrass Substitution Wikipedia
Identities involving trig functions are listed below Pythagorean Identities sin 2 θ cos 2 θ = 1 tan 2 θ 1 = sec 2 θ cot 2 θ 1 = csc 2 θ Reciprocal Identities In this video, we are going to derive the identity for the tangent of 2xThe identity for tan(x y) has been explained in the following videohttps//youtub The identity you listed might be useful if you chose the latter to rewrite the lefthand side, but it would turn out to be more complicated The alternative is to rewrite the righthand side in terms of ##2x## Then as you discovered, the identity @Office_Shredder pointed you to is useful As you get more practice, you'll develop an intuition for



Prove The Identity Secxcscx Tanx Cotx 2 Tan 2x Cot 2x1 Apply The Distributive Property2 Apply The Brainly Com



Simplify The Trigonometric Expression Tan 2x Tan X Using Double Angle Identities A Brainly Com
The trigonometric identity `(tan^2x)/(1tan^2x) = sin^2x` has to be proved Start with the left hand side `(tan^2x)/(1tan^2x)` Substitute `tanx = sin x/cos x`In the exercise that follows, you are asked to evaluate the sine or cosine of a halfangle given some information about the angle Some of the answers in this exercise involve a radical under a radical (sometimes called a nested radical)Because of the difficulty in inputting such expressions, you are only to compare the answer you work out with that of the computer$$2\\cot4x = \\cot2x \\tan2x$$ Thank you in advance Thank you for the comments and hints I got an answer after many tries ;) Below is my




5 2 Verify The Following Trigonometric Identities A Chegg Com




Analytic Trig Ppt Video Online Download
Yes, sec 2 x−1=tan 2 x is an identity sec 2 −1=tan 2 xMath\sin^2x\cos^2x=1/math math\implies\dfrac{\sin^2x}{\cos^2x}\dfrac{\cos^2x}{\cos^2x}=\dfrac{1}{\cos^2x}/math math\implies\left(\dfrac{\sin x}{\cos xNow use the identity to get the denominator in terms of cosine Multiply the first fraction by the reciprocal of the second fraction Get tangent in terms of sine and cosine 1 or (tan^2(x)1)(tan^2x1) then i'm stuck!




Integrate Tan 2x By Parts
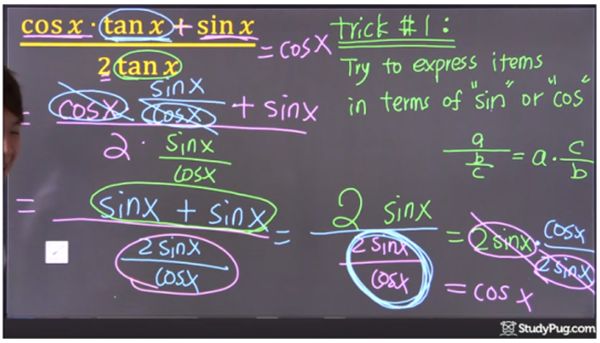



How To Prove Quotient And Reciprocal Identities Studypug
DOUBLEANGLE IDENTITIES sin(2x)=2sin(x)cos(x) cos(2x) = cos2(x)sin2(x) = 2cos2(x)1 =12sin2(x) tan(2x)= 2tan(x) 1 2tan (x) HALFANGLE IDENTITIES sin ⇣x 2 ⌘ = ± r 1cos(x) 2 cos ⇣x 2 ⌘ = ± r 1cos(x) 2 tan ⇣x 2 ⌘ = ± s 1cos(x) 1cos(x) PRODUCT TO SUM IDENTITIES sin(x)sin(y)= 1 2 cos(xy)cos(xy) cos(x)cos(y)= 1 2 cos(xy)cos(xyB) (tanx 1)(tanx1)/1 tan^2(x) = (sinx/cosx 1)(sinx/cosx 1) / 1/cosx then again I'm stuck!The Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)




F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2
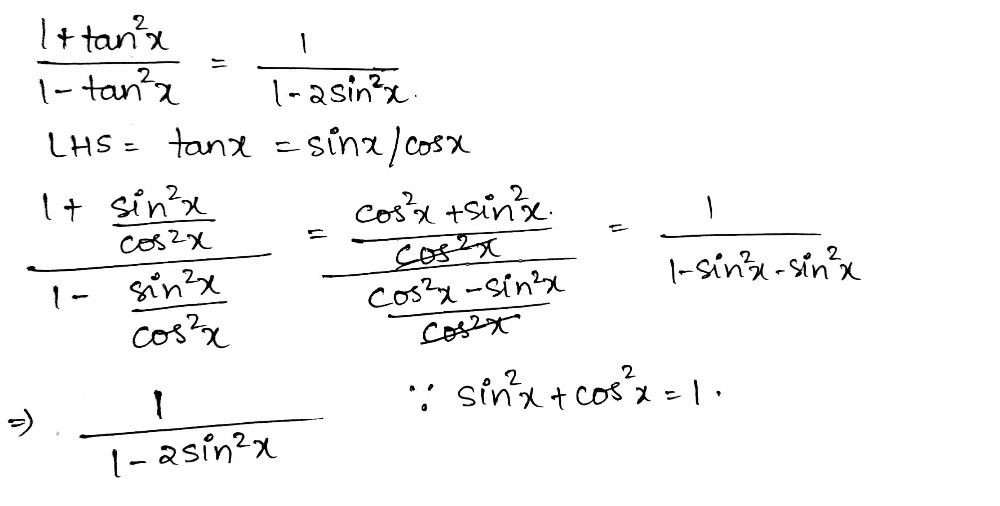



3 Prove The Following Identity 4 3 1 Frac 1 Tan Gauthmath
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Sec X Tan X OA Sec2xtan 2x Secx Tan X Sec 2x = Sec X Tan X Tan 2x Sec 2x Tan 2x Sec?xtan 2x Secxtan X OBA trigonometric identity that expresses the expansion of cosine of double angle in cosine and sine of angle is called the cosine of double angle identity Introduction When the angle of a right triangle is denoted by a symbol theta, the cosine and sine of angle are written as $\cos{\theta}$ and $\sin{\theta}$ respectively In the same way, the



A Trig Identity




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
Tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Question Prove each identity tan^2x sin^2x = tan^2xsin^2x Answer by greenestamps (8707) ( Show Source ) You can put this solution on YOUR website!Transcribed image text Verity the identity tan^2x sin^2 cos^2x = secºx To verify the identity, start with the more complicated side and transform it to look like the other side Choose the correct transformations and transform the expression at each step tan?zx sin 2x cos2x Factor out the greatest common factor Apply a Pythagorean identity to the sum of the second and third term
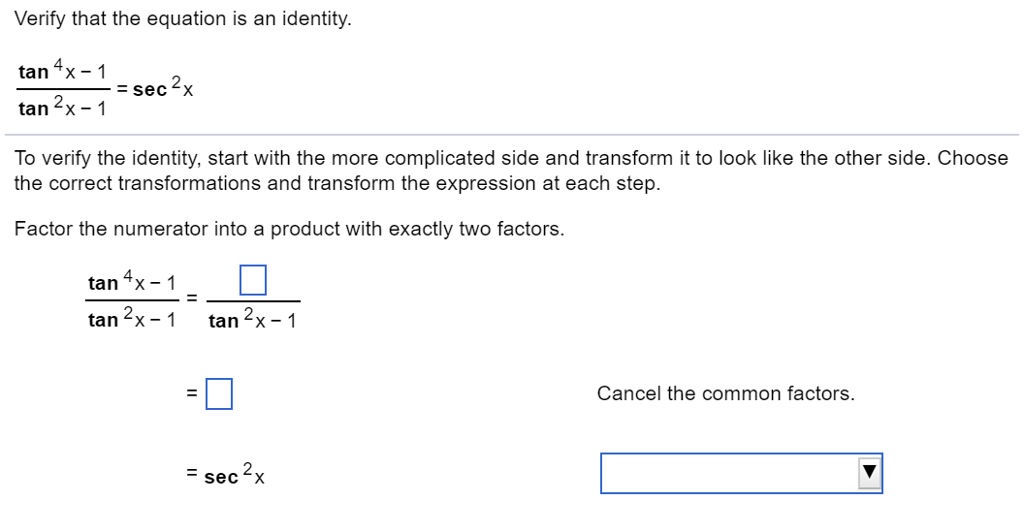



Verify That The Equation Is An Identity Tan 4x 1 Chegg Com




Integrate Tan 2x
Prove that the equation Is an identity Sec^4x Tan^4x = Sec^2x Tan^2x trigonometry Prove 1) 1 / sec X tan X = sec X tan X 2) cot A tan A = sec A csc A 3)sec A 1 / sec A 1 = 1 cos A / 1 cos A trig Yes, sec2 − 1 = tan2x is an identitySin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example \(Tan 2x =\frac{2tan x}{1tan^{2}x} \)




Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com



Ilectureonline
How do you verify the equation is an identity? Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin andAnswer to Use a doubleangle identity to find tan(2x) \ if \ sec \ x = \sqrt {14} \ and \ sin \ x < 0 tan(2x)= By signing up, you'll get




1 8 Verify Each Identity 1 Tan Sin Cos Sec Chegg Com



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero
How to prove the trigonometry equation is an identity?Sec 2 x 1 an identity? When trying to prove trig identities, it is often helpful to convert TAN functions into SIN/COS functions Proof Step 1 Start with the original equation to prove tan 2 x sin 2 x = (tan 2 x)(sin 2 x) Proof Step 2 Replace tan with sin/cos (sin 2 x/cos 2 x) sin 2 x = (sin 2 x/cos 2 x)(sin 2 x) Proof Step 3 Obtain a common denominator on left, simplify right (sin 2 x sin 2 x cos 2 x




Art Of Problem Solving




Match Expressions In Columns A And B That Complete Chegg Com
Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1A follow up proof to accompany sin^2 cos^2 =1 Another identity that is used quite a bit, especially in calculus involving trigonometric functions
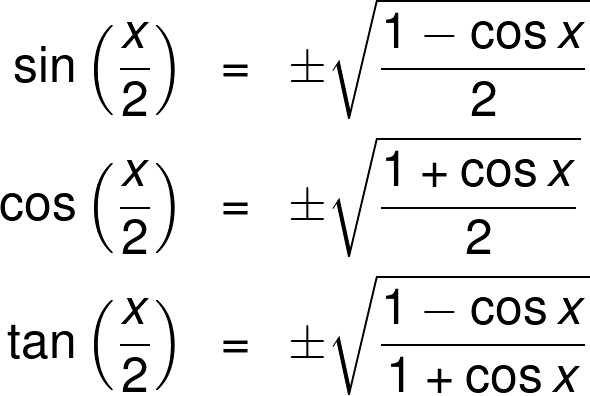



Half Angle Calculator




Chapter 11 Trigonometric Identities And Equations 11 1



Cos2x Identity




Trig Identity Sec2x Minus Tan2x T10 Youtube
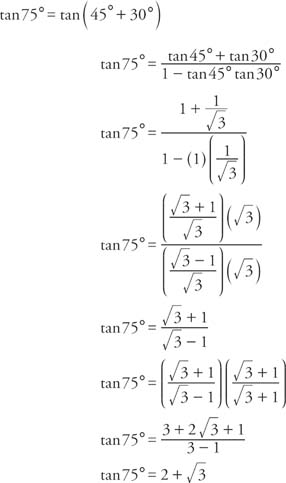



Tangent Identities




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube



3




Trig Identities And Formulas Pre Calculus Quiz Quizizz




The General Solution Of The Equation Tanx Tan 2x Tan 2x Tanx 2
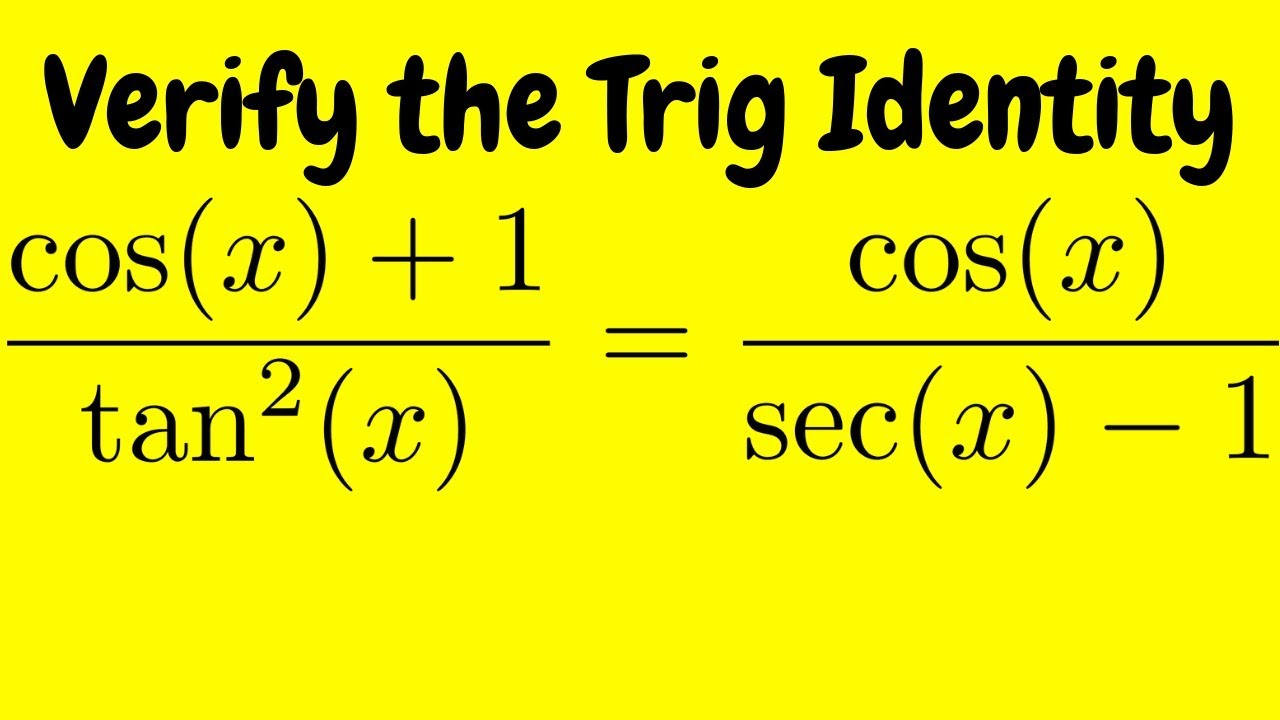



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Tan2x ただの悪魔の画像



6 1 2 Trigonometric Identities




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Prove That Cos2x Cos 2x Sin 2x 2cos 2x 1 1 2sin 2x 1 Tan 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community



Biomath Trigonometric Functions



3




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic
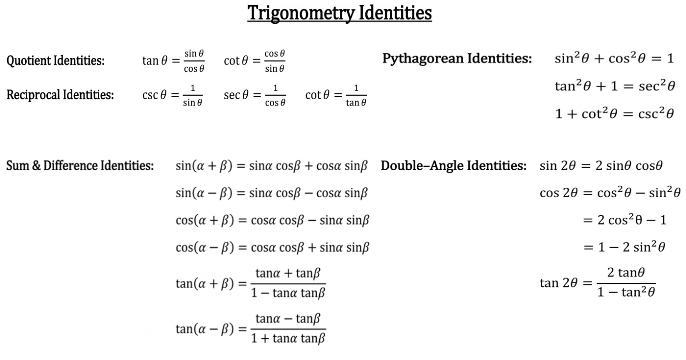



How To Prove Quotient And Reciprocal Identities Studypug



Ilectureonline




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube
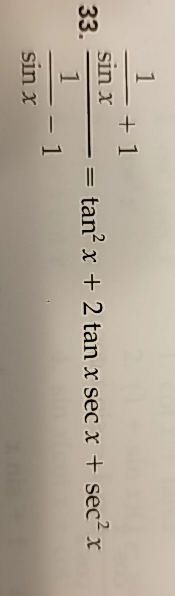



Verify The Identity Math Frac Frac 1 Sin X 1 Frac 1 Sin X 1 Tan 2x 2 Tan X Sec X Sec 2x Math Homework Help And Answers Slader




14 2 Trigonometric Identities




Tangent Half Angle Formula Wikipedia




Tangent Half Angle Formula Wikipedia



Solution Show All Steps Necessary To Verify The Trigonometric Identity 1 Tan 2x Csc 2x Tan 2x




Sum And Difference Identities Video Lessons Examples And Solutions



1



1




Integrate Sec 2x Method 2




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




How To Prove Math Tan 2 X Sin 2 X Tan 2 X Sin 2 X Math Quora
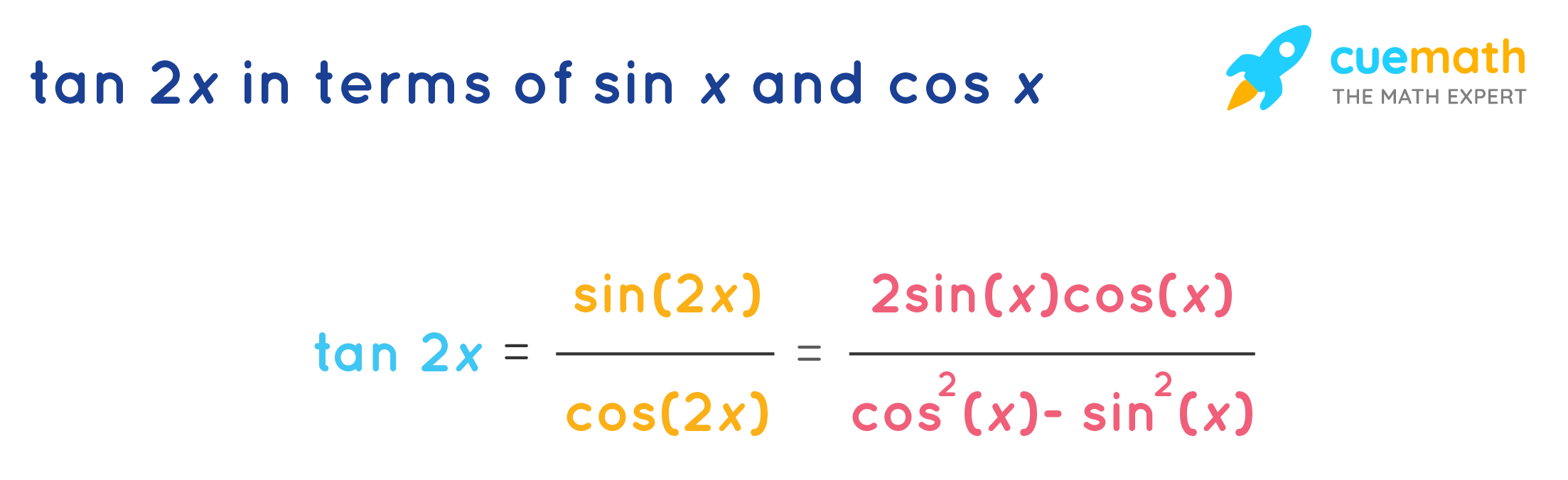



Tan 2x Formula What Is Tan 2x Formula Examples
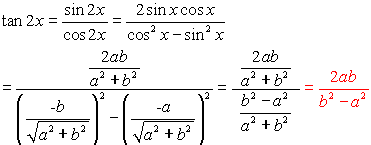



Six Trigonometric Functions Mathbitsnotebook Ccss Math
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Ch Ppt Download



Bestmaths Online Proof 4




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity



Biomath Trigonometric Functions



True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com




Double Angle And Half Angle Identities Example Sin 28 Cos 2a Or Tan 2x




Double Angles Identity Is Part Of Trigonometry Identity




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube




Double Angle Trig Identities Quiz Quiz Quizizz
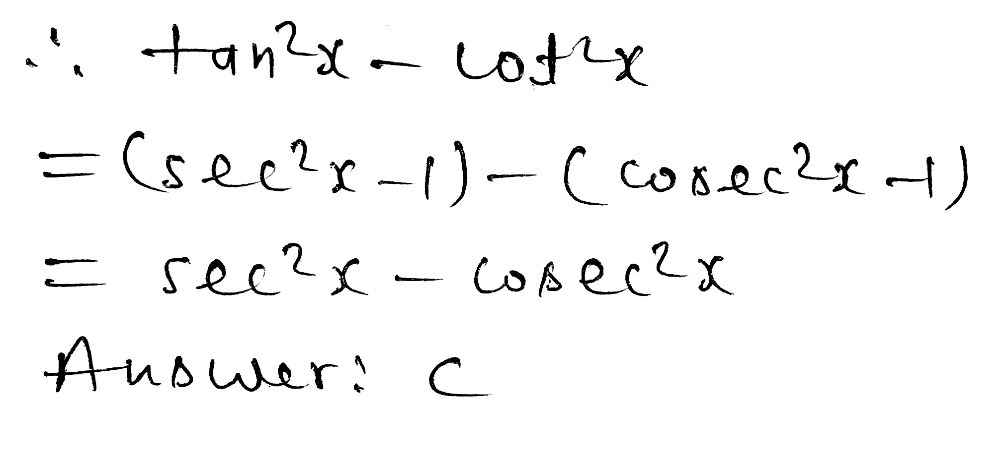



Use Trig Identities To Simplify Tan 2x Cot 2x A Gauthmath




Tan 2x Cot 2x 2




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Double Angle Properties Rules Formula Examples Video Lesson Transcript Study Com




Weierstrass Substitution Wikipedia




Verify That The Equation Is An Identity Tan 2x Cot Chegg Com




Integrate Sec 2x Method 1



Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf




Trig Double Identities Trigonometric Double Angle Functions Trig



Sin 2x Cos 2x And Tan 2x
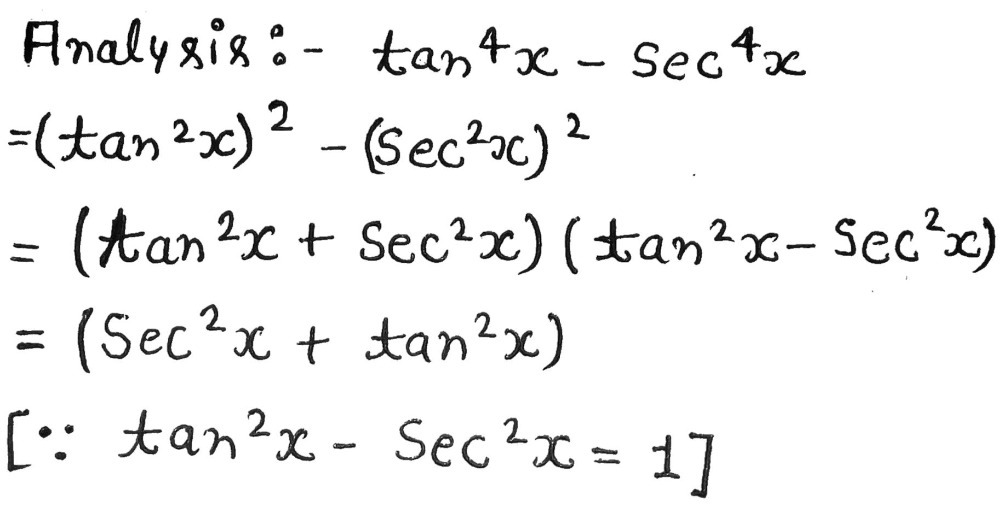



Complete The Identity Tan 4x Sec 4x Sec 2x Tan 2 Gauthmath




How To Use Trig Identities Mathematics Stack Exchange




Use The Following Information To Determine Tan 2x Tan X And Sin X Is Positive V3 Homeworklib
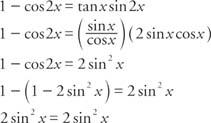



Double Angle And Half Angle Identities




Solved The Equation Tan 2 X 5 Tan X 6 0 Is A




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com




Answered Verify The Identity 2 Tan X 1 Bartleby



1 Point If Tan X 1 3 Cosx 0 Then Sin 2x Cos 2x Homeworklib



Trig Identities Hsn Forum




9 1 Identities And Proofs Ppt Download




2sinxcosx Trig Identity Gamers Smart




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic




Verify The Identity 4 2 Tan X Secx2tan X 1 Which Chegg Com
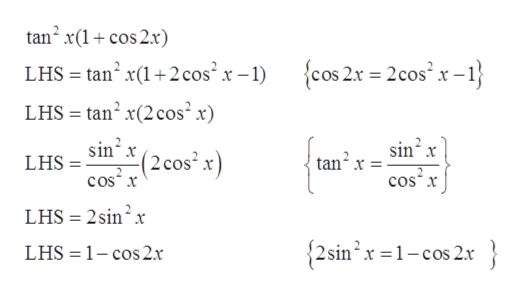



Answered Tan2x 1 Cos2x 1 Cos2x Verify The Bartleby




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
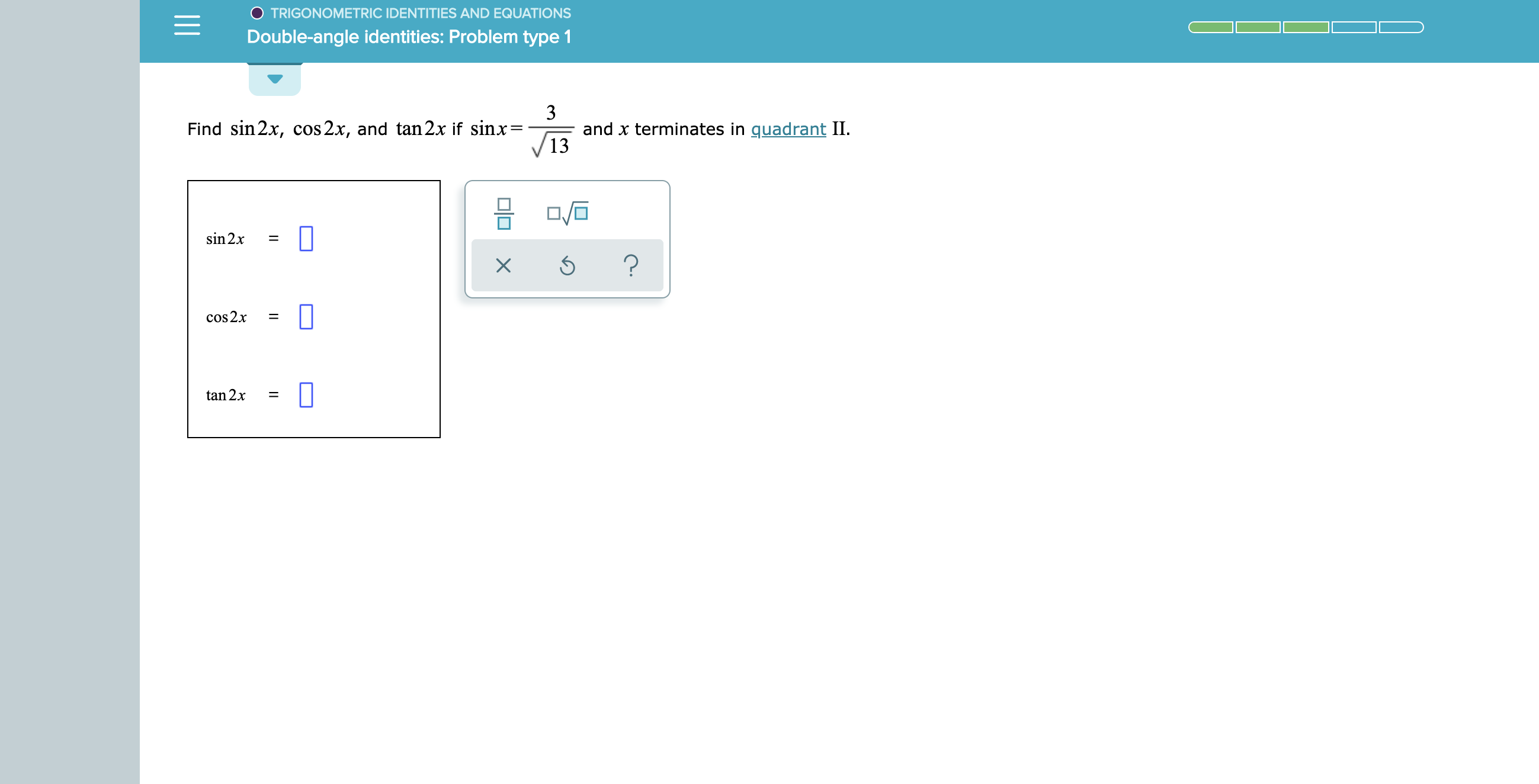



Answered Trigonometric Identities And Equations Bartleby




Pin On Youtu Be Cujsskpaulg



Solved Review The Following Derivation Of The Tangent Double Angle Identity The Steps Are Not Listed In The Correct Order Course Hero



0 件のコメント:
コメントを投稿